Project VISNUE
Eindverslag november 2001
project OOI99/03
A. Bultheel, M. Van Barel
15 november 2001
http://www.cs.kuleuven.be/~nalag/research/ALpubs/AL11.abs.shtml
Samenvatting:
Het OOI project VISNUE OOI99/03 is gestart in september 1999 en heeft als doel
om de inleidende vakken numerieke wiskunde in de faculteiten toegepaste wetenschappen en wetenschappen om te vormen tot
een praktisch vak waar de theorie vanuit de toepassingen benaderd wordt
en matlab en maple als een integraal deel van de cursus wordt opgenomen.
Er wordt een webgebaseerd platform voorzien met een discussieforum,
een vragentrommel,
de mogelijkheid van experimenteren en het voorzien van java-applets en
maple en matlabcode daartoe, het oplossen van allerlei vragen,
informatie en feedback over de
oefeningen, en externe links met professionele software en andere interessante
informatie die verband houdt met numerieke wiskunde.
In een aantal appendices wordt verwezen naar voorbeelden.
Het project is gericht op studenten van ``basiscursussen numerieke wiskunde''
die zowel in de faculteit Wetenschappen als in de faculteit
Toegepaste Wetenschappen worden gedoceerd. Het gaat specifiek om
- Numerieke wiskunde (2KBir) A. Bultheel
- Numerieke wiskunde (2KWisk+2KInf) M. Van Barel
- Numerieke wiskunde (GAS info + ind.ing.) M. Van Barel
Het doel is om over te schakelen op een ander leerproces waarbij
de studenten aangezet worden om te studeren in de lijn van de paradigma's
vooropgesteld door de ideeën van begeleide zelfstudie.
Daartoe worden middelen gecreëerd die dit moeten stimuleren en mogelijk maken.
Die omvatten o.a. het volgende
- Het ter beschikking stellen van een
``vragentrommel'' waar de studenten via elektronische weg ten allen tijde
vragen kunnen stellen over de cursus/oefeningen edm.
- Het ter beschikking stellen van een ``discussie-forum'' waar de studenten
steeds kunnen discussiëren over een probleem dat in de cursus ter sprake
gekomen is.
- Het beschikbaar stellen van een aantal illustraties onder de vorm van
applets, of maple of matlabcode waarmee de studenten kunnen experimenteren
om praktische ondervinding en inzicht op te doen rond numerieke problemen.
Sommige toepassingen zijn meer uitgewerkt en leggen de link met andere cursussen
(natuurkunde, mechanica, edm).
- Het aanbieden van extra oefeningen en inzichtsvragen die niet altijd
van academische aard zijn en/of soms van het open-einde type zijn.
Hierdoor kan de student zijn kennis, inzicht en kritische instelling
aanscherpen.
- Links worden voorzien naar meer professionele software die de student
zou kunnen gebruiken als hij later (verdere cursussen, thesis of zelfs in het
beroepsleven) numerieke problemen zal moeten oplossen.
- Een automatisch testsysteem moet de student toelaten om zijn kennis en
inzicht te toetsen. Een hint- en feedback-systeem moet de student een
automatische begeleiding geven en toelaten om zichzelf te evalueren en zichzelf
te kunnen plaatsen ten opzichte van zijn medestudenten.
Bovendien moet de lesvorm aangepast worden om de vooropgestelde
doelstelling ook te bereiken.
Er moet uiteraard ook een aangepast evaluatiesysteem gebruikt worden dat ook
de nieuwe doelstellingen van de cursus ondervraagt en quoteert.
- A. Bultheel (promotor)
- M. Van Barel (promotor)
- P. Vansevenant (projectmedewerker)
- P. Van gucht, W. Aernouts, W. Michiels, C. Demeester,
K. Depuydt, S. Gryson, S. Tastenoye (oefeningengevers)
- De resonantiegroep bestond uit de betrokken POC's (Computerwetenschappen,
Wiskunde, Informatica), de verschillende werkgroepen die binnen de faculteit
toegepaste wetenschappen met de curriculumhervorming bezig zijn en de docenten
van de numerieke vervolgvakken.
Er is van in het begin vooropgesteld dat het aanmaken
van de verschillende werkinstrumenten die hierboven zijn opgenoemd
zoveel mogelijk moet gebruik maken van bestaande systemen en expertise.
Daarom werd
eerst een overzicht gemaakt van wat er reeds in open software en gratis beschikbaar
was in de onmiddellijke omgeving en op het web
om daaruit de meest geschikte middelen te selecteren met een minimum aan
inspanning voor technische implementatie.
Daar er ook in andere universiteiten dergelijke initiatieven gaande zijn, werd
ook contact genomen met de R.U.Gent en de Universiteit Antwerpen (UIA) en werd een
gezamenlijke STIHO aanvraag gedaan ter aanvulling van het project VISNUE.
Het voorgestelde project IPON (ICT gebaseerd platform voor onderwijs in numerieke
wiskunde) werd goedgekeurd en liep in de periode 1.10.1998 - 31.10.2001 waarvan de
periode 1.1.2000 - 31.10.2001 effectief gesubsidieerd is door de Vlaamse overheid.
Op het project VISNUE is P. Vansevenant met een doctoraatsbeurs voltijds tewerk gesteld.
Het was zijn opdracht als informaticus te zorgen voor de technische ondersteuning
van het project. Na een vergelijkend marktonderzoek heeft hij de verschillende
elementen samengebracht tot het huidige platform.
Hij heeft een groot deel van zijn
tijd besteed aan het schrijven van een aantal ondersteunende applets.
Hij heeft ook een
eindwerk daaromtrent begeleid. Verder heeft hij de scripts geschreven voor het indienen
van de oefeningen via elektronische formulieren en de mogelijkheid voorzien voor
het browsen van de antwoorden. Hij was ook de contactpersoon om
met de ARIADNE groep over de ontwikkeling
van het toetssysteem te onderhandelen.
Bij al de keuzes die er gemaakt werden voor de realisatie is er steeds op
gelet dat het met een minimum aan werk voor de studenten moest kunnen gebruikt
worden (zo weinig mogelijk extra programma's installeren op de eigen PC).
Ook wilden we een draagbaar platform maken. Dit wil zeggen dat de student het
geheel kan copiëren op zijn eigen PC en dat hij alles wat redelijkerwijs
mogelijk is ook off-line kan gebruiken. Natuurlijk is dit niet vol te houden
voor de vragentrommel, het indienen van de oefeningen, het toetssysteem,
verwijzingen naar externe links, edm. Op dit ogenblik kan het systeem
in zijn geheel overgehaald, of op drie floppies gekopieerd worden.
Volgende elementen werden gerealiseerd:
- Er zijn webpagina's aangemaakt voor elk van de bovengenoemde doelgroepen.
Hiervoor kan men raadplegen
Het is belangrijk dat de student op elk moment kan zien
waar hij in het systeem is terechtgekomen, zodat hij de oorspronkelijke doelstelling
niet uit het oog verliest. We hebben daarbij gekozen voor een open en vrij
beschikbaar Javascript (joust
http://www.ivanpeters.com/)
om deze navigatie te realiseren.
Op deze cursus-web-pagina's kan men links vinden naar een aantal
belangrijke onderdelen zoals de vragentrommel, de nieuwsgroep, de oefeningen,
het toetssysteem, illustraties uit de lessen, praktische en nuttige informatie
in verband met de cursus. Daarover hieronder meer.
- Een vragentrommel.
Hiervoor werd gebruik gemaakt van de
infrastructuur van het kandidatuurcentrum waar een dergelijk systeem bestaat
voor de vakken van de eerste kandidaturen.
Kris Aerts (KC) heeft het systeem aangepast zodat het ook voor het vak
numerieke wiskunde kan gebruikt worden. Dit in 3 versies: (a) 2de kan. Burg. ir.; (b) 2de kan. Wisk./Inform.; (c) aanv. opl. informatica + ind. ir.
Vragen kunnen gesteld worden over elk van de hoofdstukken uit de cursus
en over de oefeningen. Er is een zoekfunctie voorzien waardoor alle relevante
vragen over een bepaald trefwoord kunnen opgezocht worden.
Er kan ook gezocht worden in vragen van vorige jaren.
De vragentrommels voor numerieke wiskunde zijn
bv. ook te bereiken via de webstek van het KC:
http://www.kc.kuleuven.be.
- Een newsgroup die is aangemaakt via de gewone kanalen waarmee
(interne) nieuwsgroepen via het Ludit worden gemaakt en onderhouden.
De nieuwsgroep heet
kuleuven.faculty.tw.cursus.numwis en is bv. te bereiken via de stek
van het betreffende vak.
- Een speciale link met de planning, voorbereidende tekst en feedback over
de normale oefenzittingen van het vak.
Oefeningen die in de computerklassen van de K.U.Leuven worden gepland kunnen
via een elektronisch formulier worden ingeleverd.
Voor de feedback worden de antwoorden manueel nagekeken en worden veelgemaakte
fouten anoniem besproken.
Een voorbeeld van feedback op een oefening is in bijlage gegeven.
- Informatie over hoe men de verschillende programma-codes die men aangeboden krijgt
kan laten lopen op de computers van de computerklassen of op de eigen
PC. Ook informatie over hoe de nieuwsgroep kan gebruikt worden, edm.
- Algemene (externe) links naar software of wetenswaardigheden die wereldwijd
via het internet beschikbaar
zijn. Dit is ``extra'' en kan op volledig vrijwillige
basis al of niet geraadpleegd worden.
- Een reeks van illustraties.
Dit zijn voorbeelden, sommige met een ingenieursachtergrond, waar de
numerieke technieken die in de cursus staan worden toegepast.
Op het web worden deze illustraties aangeboden door een korte beschrijving
(in html). Ze zijn gestoffeerd door het aanbieden van matlabcode,
maple code en/of java-applets.
Met deze programma's kan door de studenten geëxperimenteerd worden.
De programma's gaan ook gepaard met een reeks vragen
(soms met een open antwoord) die de student moeten uitnodigen om over de
resultaten na te denken en eventueel proefondervindelijk of via de
theoretische uitleg een oplossing of verklaring te zoeken.
Een uitgebreider voorbeeld wordt in appendix toegevoegd.
- De lessen bestaan in hoofdzaak uit demonstraties van dit soort
illustraties en toepassingen
om aldus begrippen en technieken aan te brengen. De theorie wordt slechts
kort aangehaald in de les en moet door zelfstudie aangeleerd worden met
behulp van de cursustekst.
Eventuele vragen kunnen mondeling of via de vragentrommel gesteld worden.
- Het examen.
Tijdens het eerste jaar van het project (academiejaar 1999-2000) is er
van bij het begin van het academiejaar gezegd dat de evaluatie
gedeeltelijk zou bestaan
uit een open boek gedeelte waarbij men alle oefeningen en
uitwerkingen en testen die men gedaan heeft tijdens het jaar ook mag meebrengen.
Het soort vragen zou gelijken op wat er als vragen bij de illustraties op het
web wordt aangeboden. Aldus wordt het ``dagelijks werk'' geëvalueerd.
Vermits dit een totaal nieuwe vorm van examineren was voor dit vak werd er als
overgangsmaatregel nog een gedeelte van het examen in de vorm van gesloten
boek examen afgenomen. Hier betreft het meer klassieke examenvragen die
theorie en oefeningen ondervragen die kunnen geblokt worden door op korte
termijn de cursus te studeren en zonder ooit zelf met de aangeboden middelen
te experimenteren.
Tijdens het tweede jaar van het project (academiejaar 2000-2001) is het theoretisch
gedeelte achterwege gelaten en is het examen volledig open boek geworden waarbij
men alles mocht meebrengen wat men aan documentatie in de loop van het jaar had
verzameld.
Een voorbeeld van zo een examen is ook als appendix toegevoegd.
- De toets- en testomgeving.
Zoals beschreven is er een stel van vragen voorzien bij de illustraties.
Er is echter geen feedback en ook geen formeel vraag-en-antwoord systeem voorzien.
Daarom is er gekeken naar bestaande toetsplatformen (ARIADNE en USolv-IT)
Vermits USolv-IT weer een extra browser vergde om te installeren en het een
groot systeem was dat dus wat logger te manipuleren was en buiten het bereik
kwam van het project, werd er gekozen voor een ARIADNE-achtige aanpak.
Vermits op het departement alle expertise in huis was om het systeem aan onze
noden aan te passen leek dit het meest geschikte systeem.
Vooral dank zij Raf Van Durm werd een aanpassing gemaakt die een
volledig op LATEX en XML gebaseerde invoer toeliet.
LATEX is immers het middel om wiskundige teksten in te tikken
en het laat toe om op een handige manier figuren toe te voegen.
Met een eenvoudige Latex2html omzetter en een webserver die xml 1.0 kan parsen
kan het systeem klaargemaakt worden voor een web-browser.
Het beheer en de behandeling van de commando's van de gebruiker wordt php code
gerealiseerd.
![\begin{displaymath}
\includegraphics[width=8cm,height=8cm]{meta1}
\end{displaymath}](img5.gif)
De opsteller van de vragen kan eventueel een hint meegeven die de student
kan opvragen. Ook is er voor het oplossen van de vragen een permanente
mogelijkheid om het formularium op te vragen en om een overzicht te krijgen
van de verschillende mogelijke types van vragen en hoe die moeten beantwoord
worden.
De volgende types vragen zijn mogelijk:
- Word question.
Hier wordt een woord als antwoord verwacht. Het woord moet daarbij natuurlijk correct gespeld
zijn. De score bij dit type vraag is dan 0 of 10.
- Numerical question.
Bij dit type wordt er een getal verwacht waarop er een procentuele afwijking kan zitten. Maar
meestal is die afwijking gelijk aan 0. Dit is dus ook een alles of niets vraag (0 of 10 punten).
- Fill-in question.
Hier worden er een aantal getallen en/of woorden verwacht. Per correct onderdeel krijg je (10 /
aantal onderdelen) punten. Voor een verkeerd antwoord worden er geen punten afgetrokken.
Voorlopig worden geen getallen met komma's aanvaard. In die gevallen ben je verplicht om een
rationaal getal als antwoord te geven. Bvb. 0.5 moet als 1/2 ingevoerd worden. Ook leidende nullen
en spaties worden als fout aangerekend.
- Radiobutton question.
Bij dit type van vraag is er maar 1 correct antwoordalternatief. Voor een goed antwoord krijg je 10
punten, voor een verkeerd antwoord worden er (10 / aantal foutieve antwoordalternatieven) punten
afgetrokken zodat gokken weinig zinvol is. Een open antwoord is mogelijk zolang er niets werd
geselecteerd.
- Multiple-choice question.
Bij dit type van vraag zijn er dus 1 of meerdere correcte antwoorden mogelijk. Per goed
deelantwoord krijg je (10 / aantal juiste alternatieven) punten. Voor elk verkeerd deelantwoord
worden er (10 / aantal foutieve alternatieven) punten afgetrokken.
De student kan ook steeds een e-mail
sturen naar het didactisch team indien hij dit zou wensen.
Voor het didactisch team is er de mogelijkheid om de scores van de studenten
op te vragen voor de verschillende vragen. De student kijgt bij zijn antwoorden
steeds de maximale score bij een vraag, de door hem behaalde score en een gemiddelde
waarde die door alle voorgangers op deze vraag behaald werd.
Voor het didactisch team wordt het mogelijk de moeilijkheidsgraad van een
vraag te herzien indien de score onverwacht hoog of laag zou zijn.
- Via de faculteit en het departement computerwetenschappen is een financiële
inspanning gedaan om aan elke student tegen een minimale vergoeding
de matlab en maple CD's af te leveren. Maple is verdeeld via het departement,
matlab via VTK.
- Dank zij het project VISNUE, hebben we ook aktief deel kunnen nemen aan het
STIHO project IPON (ICT gebaseerd platform voor onderwijs in numerieke
wiskunde).
De hoofdpromotor is de R.U.Gent, de derde partner is de Universiteit Antwerpen
(UIA).
Het project IPON werd goedgekeurd met een globaal budget van 5.000.000 BEF en
liep in de periode 1.10.1998 - 31.10.2001 waarvan de
periode 1.1.2000 - 31.10.2001 effectief gesubsidieerd is door de Vlaamse overheid.
Het systeem van de vragentrommel is uitgewisseld met Gent en Antwerpen.
Antwerpen belooft een interface te schrijven voor een virtuele
machine die ze ontwikkeld hebben waarop numerieke berekeingen in verschillende
basissen en net verschillende nauwkeurigheid en afrondingsregels kunnen
uitgevoerd worden. Dit is duidelijk een informatica-project.
Voor onze studenten numerieke wiskunde willen we zoveel als mogelijk van de
programmeeraspecten afschermen. Vandaar de nood aan een interface die
dat realiseert. Op het ogenblik dat dit eindverslag geschreven wordt
is deze interface nog niet beschikbaar.
VISNUE heeft van R.U.Gent (project ILONA) een aantal applets zonder problemen
kunnen overnemen. Die werden naast de eigen applets in het systeem ingebracht.
De webpagina van het project IPON is
http://www.cs.kuleuven.be/~nalag/teaching/ipon/
- In het academiejaar 2000-2001 is een nieuwe cursus G188/X162:
Computergesteund probleemoplossen in de natuurkunde ingericht
voor de 2de kandidatuur natuurkunde.
De titularis R. Cools heeft van het stramien van de VISNUE sites gebruik
gemaakt om een analoge site te maken voor zijn vak. Dit ging zonder problemen
en is het eerste jaar al gebruikt.
De stek van deze cursus is
http://www.cs.kuleuven.be/~ronald/G188/.
Nog niet alles is definitief, maar toch kunnen
we reeds volgende vaststellingen doen.
- De vragentrommel wordt goed gebruikt (146 vragen 2KBir voor 1999-2000 en
70 vragen in 2000-2001).
Het vak voor 2KBir wordt gedoceerd gedurende het eerste semester plus de eerste
7 weken van het tweede semester. Het examen is in juli.
Opvallend is dat men uit de frequentie van de vraagstellingen
kan opmaken dat men pas het vak begint te blokken rond de paasvakantie.
Een piek valt tijdens de klassieke blok periode.
Het examengebeuren is dus nog steeds een kwestie van blokken en niet van
evaluatie van werk tijdens het jaar. Men stoomt zich nog steeds klaar voor
een examen. Deze vaststelling was sterker in het eerste jaar van het project.
Waarschijnlijk heeft dit iets te maken met de onzekerheid van de studenten
over hoe nu zo een ``nieuw'' examen zou verlopen. Tijdens het tweede jaar
van het project is deze tendens nog steeds aanwezig maar al veel minder
uitgesproken en zoals hierboven vermeld, waren er ook veel minder vragen.
- De nieuwsgroep is nagenoeg niet gebruikt.
Tijdens de les en in sommige antwoorden in de vragentrommel is de suggestie
gemaakt dat men een discussie zou kunnen houden over het probleem in de
nieuwsgroep. Dit heeft echter niet het verhoopte gevolg gehad.
In een nieuwsgroep van de jaren, meer specifiek 2KInf, is er wel een
geanimeerde discussie geweest over het vak en de cursusnota's, maar niet
over numerieke vraagstukken. Voor andere vakken (bv. Informatieoverdracht
in 2KBir) is er wel een (gemodereerde) goed werkende discussiegroep.
Navraag bracht aan het licht dat de vragen reeds ``op kot'' werden
bediscuteerd en een oplossing hadden gevonden zodat men een discussie
op het web (met moeilijkheden wat betreft wiskundige notatie) als overbodig
beschouwd werd.
- De toepassingen die bij de illustraties gebruikt zijn (voor 2KBir)
behandelen problemen als convectie-diffusie, warmtevergelijking,
transportvergelijking, Laplacevergelijking, de gedempte slinger.
Uit de natuurkunde werd in overleg met collega Lauriks het voorbeeld
voor het oplossen van de Schrödingervergelijking genomen.
In verband met de cursus mechanica werd op voorstel van collega
G. Van der Perre de vergelijking
van een slinger met vrij glijdend ophangpunt in applet-vorm gegoten en op voorstel
van collega R. Piessens werd in verband met de cursus analyse een applet voor de illustratie van gelijkmatige
continuïteit gemaakt in het kader van een eindwerk.
Verder komen aan bod de Randles-Sevcik functie uit elektro-chemische toepassingen,
een chemische bellenreactor, het effect van een aardbeving op een gebouw,
en een thermisch probleem.
Dit heeft zeker de horizontale integratie bevorderd. Er zijn nog vragen gekomen
van andere collega's om nog voorbeelden die geen analytische oplossing hebben
op een numerieke manier te behandelen in de cursus numerieke wiskunde.
Of dit ook daadwerkelijk zal gebeuren is te betwijfelen gezien door de hervormingen
in het kader van het Bachelor-Master systeem alles weer op losse schroeven wordt gezet.
Deze toepassingen zijn erg belangrijk omdat ze een samenhang tussen
verschillende vakken geven en erg motiverend werken voor het vak
numerieke wiskunde.
Ze worden telkens gebruikt om een andere numerieke techniek te illustreren.
Het is niet altijd gemakkelijk voorbeelden en toepassingen te vinden die
nog bevattelijk zijn op kandidatuursniveau.
Het is niet de bedoeling dat te veel technische zaken in illustraties het
aanleren van de nieuwe numerieke techniek bemoeilijken.
Voor de 2KW/I is het nog moeilijker om dergelijke voorbeelden te vinden
gezien dit soort ingenieursvakken met toepassingen niet voorhanden zijn.
Hier wordt dan ook gekozen voor meer academische illustraties.
- Voor de lessen was er eerst een grote belangstelling, maar naargelang
het jaar vorderde nam de interesse af. Het gevolg is dat veel van wat in
de lessen gezegd is geweest, later (tijdens de blokperiode) nog eens
moest herhaald worden als antwoord op een vraag gesteld in de vragentrommel.
We denken dat er nog te veel wordt ``geblokt voor het examen''.
Er zou een regelmatiger studiepatroon moeten komen.
Mits voldoende inspanning tijdens de doceerperiode van het vak zou het
echte ``blokken'' eigenlijk moeten wegvallen.
Vermits deze inspanning doorgaans niet geleverd wordt, haakt men ook af
voor de lessen. De student is dikwijls ``niet mee''.
We hebben goede hoop dat met het invoeren van het semestersysteem
hier grotendeels aan zal verholpen worden.
Tot 2000-2001 was er nog steeds een juli-examen over stof die veel
voeger gezien is en dat kan de interesse niet
opwekken gedurende het eerste semester.
- We herhalen hier een toch wel merkwaardig fenomeen dat we reeds in het
tussentijds rapport hebben vermeld.
Omdat een automatische toetsomgeving nog niet bestond in het eerste
projectjaar en om de onzekerheid
bij de studenten over de examenvorm wat weg te nemen is er een aangekondigde
toets tijdens
de les gedaan (2KBIr) in november 1999. Bijna niemand wist het hele antwoord.
In plaats van de oplossing te geven is gesuggereerd om hierover de
discussiegroep of de vragentrommel te gebruiken. Dit zonder veel resultaat.
Een maand later werd dezelfde vraag gesteld tijdens een onaangekondigde
toets. Nagenoeg niemand had ondertussen over het antwoord nagedacht.
- Een zeker nadeel van dit systeem is dat het niet
geïntegreerd is in een groot geheel (zoals bv. Blackboard) maar dat heeft
nu net het voordeel dat het heel erg draagbaar is en gemakkelijk te onderhouden.
Het is trouwens niet moeilijk om een aantal elementen uit het systeem te nemen
die reeds in een systeem als Blackboard aanwezig zijn en het overige materiaal
binnen Blackboard aan te bieden. We benadrukken nogmaals dat het ontwikkelde
systeem zeer compact en gratis is, en op een aantal minder belangrijke toeters
en bellen, nagenoeg dezelfde functionaliteit heeft als een groot en duur
systeem. Daartegenover staat dat het kan draaien zonder extra installatie van
programma's en dat het (voor zover dat redelijk mogelijk is)
onafhankelijk is van een internetverbinding.
Op vraag van de studenten is een gezipte versie van de hele site beschikbaar
gemaakt zodat ze alle informatie op 3 floppies kunnen kopiëren en
thuis op een eigen computer off-line de bestanden kunnen bekijken.
Het gehele systeem is slechts 3MB groot.
- Veel tijd moet gestopt worden in het overtuigen van en uitleggen aan de
studenten van het opzet
van deze aanpak. Uit discussies en gestelde vragen blijkt nog steeds dat
de student de docent ziet als een potentiële vijand die eigenlijk alleen
maar een hinderpaal is om een diploma te behalen.
Het vraagt een hele mentaliteitsverandering bij studenten om aan te nemen dat
zijzelf degenen zijn die het diploma willen behalen en daar dan ook zelf de
verantwoordelijkheid moeten voor nemen, en dat de docent
(en het hele onderwijsteam) hen daarbij zoveel mogelijk middelen ter beschikking
stelt. De student moet op verantwoorde manier een keuze uit die
middelen maken. Dit vergt meer dan een jaar om de studentenpopulatie hiervan te
overtuigen. Bewijs hiervan is
de ongerustheid en onzekerheid bij de studenten over het examen
die gedurende het tweede projectjaar al heel wat minder was dan het eerste jaar.
Blijkbaar waren de studenten door hun voorgangers gerustgesteld.
- Het bestaan van de web-omgeving enerzijds en de cursustekst anderzijds
geeft een bifocaal gevoel voor de studenten waarbij men niet meer goed weet
aan wat men zich moet houden en wat er nu eigenlijk moet gekend zijn.
Het integreren van de twee in een documentatie van x aantal studiepakketjes
zou dit kunnen verduidelijken en bevattelijker maken.
Het was de bedoelling om tegen het academiejaar 2001-2002 een tekst met een
(multimediale) CD klaar te hebben waarin deze dualiteit zou wegvallen.
Vermits er voor het Bachelor-Master systeem (2002-2003?)
echter voorzien wordt dat het vak de helft zal
verminderen in volume, denken we dat het niet erg rendabel is om voor
1 jaar de hele hervorming door te voeren.
- De gevolgde aanpak vraagt duidelijk veel meer inspanning van de docent
en van het begeleidingsteam voor de oefeningen.
Het is voor de docenten een zeer leerrijke ervaring om het vak op
deze manier te geven.
Er is veel tijd besteed aan het nadenken over de aanpak van de lessen en
de evaluatie. Die reflectie werpt duidelijk vruchten af.
Uit bovenstaande commentaar en bedenkingen volgt dat de mentaliteitsverandering
bij de studenten nog moet groeien in de richting van begeleide zelfstudie.
We denken dat een of andere vorm van permanente evaluatie en/of een
kalendersysteem daarom aangewezen is.
- De hele documentatie is beschikbaar op het web via de bovengenoemde en
onderstaande links.
Dit kan door iedereen vrij gebruikt worden.
Er komen dan ook soms vragen toe van middelbare scholen of scholen in
Nederland.
- Tijdens een departementsraad is een uitvoerige uiteenzetting gegeven
over het project waarbij vooral de doelstellingen, de realisaties en de
moeilijkheden werden aangehaald.
- Er is een voorstelling gedaan van het project voor de POC kandidaturen toegepaste
wetenschappen.
- Er zijn verscheidene pogingen geweest om het project ook voor te stellen op de
POC informatica. Door omstandigheden is dit een aantal keren moeten uitgesteld
worden en is ten slotte omwille van drukke bezigheden in verband met SES en
BaMa systeem niet kunnen plaats hebben.
- Er is contact opgenomen met collega's in verband met de illustraties.
De bedoeling is dat ze ook naar de toepassingen en de numerieke
technieken zullen verwijzen in hun cursus.
- Er is een artikel verschenen in de Campuskrant jaargang 11, nummer 9, juni 2000
waarin het project wordt voorgesteld.
- Er is een STIHO aanvraag gedaan en goedgekeurd met de naam IPON.
Het project VISNUE is een onderdeel hiervan. Aan dit project nemen ook
de Universiteit Gent en de Universiteit Antwerpen deel.
Applets en andere elementen van het platform werden uitgewisseld.
- De ontwikkelde java-applets worden ook via het ooi project van P. Igodt
ter beschikking gesteld aan alle gebruikers van dat systeem (alle eerste
jaarsvakken wiskunde aan kulak en K.U.Leuven).
- Er is voorzien in een technische documentatie van alle elementen
die in het platform werden geïmplementeerd
(zie rapporten AL13 en AL14 op http://www.cs.kuleuven.be/~nalag/research/ALpubs/)
en van de java-applets die ontwikkeld zijn door de projectmedewerker
(zie
http://www.cs.kuleuven.be/~nalag/demos/visnue/).
- http://www.cs.kuleuven.be/~ade/WWW/NW/
webstek van het vak voor 2K Bir. (A. Bultheel)
- http://www.cs.kuleuven.be/~marc/NumWis/Menu/indexG033.htm
webstek van het vak voor 2KW+I (M. Van Barel)
- http://www.cs.kuleuven.be/~marc/NumWis/Menu/indexH302.htm
webstek van het vak voor GAS Inf+ind.ing. (M. Van Barel)
- http://www.cs.kuleuven.be/~ronald/G188/. webstek voor ket vak voor 2K Natuurkunde (R. Cools)
- http://www.kc.kuleuven.be/
webstek van het kandidatuurcentrum toegepaste wetenschappen.
- http://www.cs.kuleuven.be/~nalag/demos/visnue/
webstek van binnen visnue ontwikkelde applets.
- http://www.cs.kuleuven.be/~nalag/teaching/ipon/
de webpagina van het project IPON.
- Site map numerieke wiskunde 2KBir.
Zie de index frame van
http://www.cs.kuleuven.be/~ade/WWW/NW/.
- De vragentrommel 2KBir.
Zie
http://www.kc.kuleuven.be/numwis-burg/vragen1999/index.pht.
- Voorbeeld van een toepassing. Zie de slinger-vergelijking
http://www.cs.kuleuven.be/~ade/WWW/NW/NW/wagenslinger/index.html.
- Voorbeeld van opgaven.
Zie oplossen van stelsels met Gauss. Zie
http://www.cs.kuleuven.be/~ade/WWW/NW/NW/gauss/index.html
- Voorbeeld van een oefenzitting. Zie
http://www.cs.kuleuven.be/~ade/WWW/NW2/archief/oef0001/oefz10/index.html
- Voorbeeld van feedback na oefenzitting. Zie
http://www.cs.kuleuven.be/~ade/WWW/NW2/archief/oef0001/Oefz10/beschouw0001/index.html
- De java-applets ontwikkeld in VISNUE. Zie
http://www.cs.kuleuven.be/~nalag/demos/visnue/
voor de webstek van binnen visnue ontwikkelde applets.
- De webstek van het STIHO project IPON. Zie
http://allserv.rug.ac.be/~mvdaele/cgi-bin/Ipon/Ipon.html
voor de webstek van het project.
- Bijlage 9: Een voorbeeld van een examen.
NUMERIEKE WISKUNDE 2eKAN OPEN BOEKJuli 2001
- De differentievergelijking
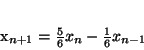 |
(1) |
heeft oplossingen
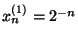 als de startwaarden zijn
als de startwaarden zijn 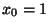 en
en 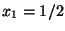 , en
, en
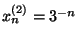 als de startwaarden zijn
als de startwaarden zijn 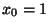 en
en 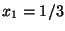 .
.
De oplossingen worden berekend (in eindige precisie) met de recursieformule
(14).
Daardoor ontstaat een relatieve fout voor de berekende 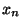 die op de bijgaande
figuur is uitgezet voor de oplossingen
die op de bijgaande
figuur is uitgezet voor de oplossingen 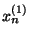 en
en 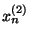 (log-schaal).
(log-schaal).
- Eén van de curven stijgt linear. Dewelke, die voor
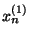 of die voor
of die voor 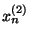 ?
?
- Verklaar de helling (rico) van die rechte.
- Waarom blijft de fout voor de andere oplossing wel beperkt?
- Is de stijgende fout veroorzaakt door de conditie van het probleem,
vergelijkbaar met de conditie van een differentiaalvergelijking
(inherente onstabiliteit van de vergelijking) of heeft dit iets te maken
met de onstabiliteit van de numerieke berekening en wordt dit veroorzaakt door
een sterk accumuleren van de afrondingsfouten?
- Beschouw de volgende iteratieformule
We programmeren dit met de volgende matlabcode
function x = iter(a)
% de startwaarde
x=1.5;
xo=10*x;
while abs(x-xo)>eps
xo=x;
x=(x-a)^2+1;
end
We laten deze routine lopen voor de waarden 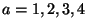 telkens met de startwaarde 1.5.
We krijgen als resultaat
de volgende grafieken
voor de logaritme van de absolute waarde van de fout.
Verklaar deze grafieken
telkens met de startwaarde 1.5.
We krijgen als resultaat
de volgende grafieken
voor de logaritme van de absolute waarde van de fout.
Verklaar deze grafieken
- In de les is een demo gegeven van een niet-lineair kleinste-kwadratenprobleem
waarbij men in het model
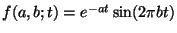 de parameters
de parameters 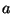 en
en 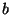 zodanig moest kiezen dat voor een opgegeven tabel
van meetwaarden
zodanig moest kiezen dat voor een opgegeven tabel
van meetwaarden
 de functie zo goed mogelijk moest
aansluiten:
de functie zo goed mogelijk moest
aansluiten:
In dit voorbeeld waren de meetpunten 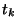 equidistant:
equidistant: t=0:0.05:1.
De contourlijnen van de som der kwadraten zijn hieronder getekend
voor het voorbeeld 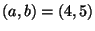 .
.
- Beschrijf expliciet de methode van Gauss-Newton voor dit probleem.
- Bereken de Jacobiaan en leg uit hoe men de correctie berekent in elke iteratiestap.
- Bereken de gradiënt voor het probleem.
Heeft men die nodig in de methode van Gauss-newton?
- Kan je iets zeggen over de conditie van het minimum?
- Is de conditie van
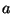 en
en 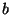 even goed of niet? Hoe kan je dat meten?
even goed of niet? Hoe kan je dat meten?
- Geef een afleiding van de gerelaxeerde Jacobi methode en leg uit hoe
men de relaxatieparameter moet kiezen.
© Adhemar Bultheel
2001-12-06
![\begin{displaymath}
\includegraphics[width=15cm,height=10cm]{hfdp}
\end{displaymath}](img1.gif)
![\begin{displaymath}
\includegraphics[width=8cm,height=8cm]{vrtr1}~~
\includegraphics[width=8cm,height=8cm]{vrtr2}
\end{displaymath}](img2.gif)
![\begin{displaymath}
\includegraphics[width=8cm,height=8cm]{vrtr3}
\end{displaymath}](img3.gif)
![\begin{displaymath}
\includegraphics[width=8cm,height=8cm]{oef1}~~
\includegraphics[width=8cm,height=8cm]{oef2}~~
\end{displaymath}](img4.gif)
![\begin{displaymath}
\includegraphics[width=8cm,height=8cm]{meta1}
\end{displaymath}](img5.gif)
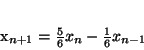
![\begin{displaymath}
\includegraphics[width=10cm,height=7cm]{/home/ade/heinz/teksten/vragen/no/f003}
\end{displaymath}](img16.gif)
![\begin{displaymath}
\begin{array}{cc}
\includegraphics[height=5cm,width=7cm]{/...
...ade/heinz/teksten/vragen/no/f044d}\\
a=3 & a=4
\end{array}
\end{displaymath}](img19.gif)
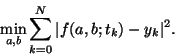
![\begin{displaymath}
\includegraphics[width=10cm,height=4cm]{/home/ade/heinz/teksten/vragen/no/f047}
\end{displaymath}](img27.gif)