T812

Promotor: Stefan Vandewalle en Paul Dierckx
Begeleider: Hendrik Speleers

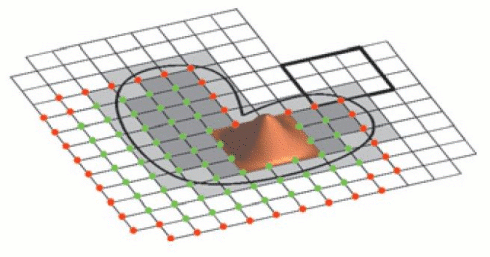
Tensor-product splines worden vaak gebruikt voor het benaderen van functies en discrete punten, computergesteund probleemoplossen, of het oplossen van differentiaalvergelijkingen. De kracht van deze splines zit hem in het feit dat ze compact voorgesteld kunnen worden met zogenaamde B-splines. Ze worden gedefinieerd op rechthoekige roosters, waarbij met iedere knoop in het rooster een B-spline wordt geassocieerd. Deze B-splines zijn verschillend van nul op een beperkt aantal deelvlakjes. Hebben we echter met een willekeurig gekromd domein te maken, dan zijn WEB-splines (Weighted Extended B-splines) meer geschikt. De gewone B-splines die gedeeltelijk binnen en buiten het gebied liggen kunnen voor stabiliteitsproblemen zorgen; de 'extended' versie verhelpt dergelijke problemen. Door aan de splines nog een passende gewichtsfunctie toe te kennen, kan er bovendien voor gezorgd worden dat aan de gewenste (homogene) randvoorwaarde voldaan is. De WEB-splines blijken heel geschikt te zijn als eindige elementen om partiële differentiaalvergelijkingen numeriek op te lossen. Enkele van de voordelen zijn:

• Er moet geen ingewikkeld rooster gegenereerd worden, wat voor andere elementen vaak tijdrovend is.
• Tensor-product B-splines kunnen efficiënt geïmplementeerd worden.
• De orde van de spline kan vrij gekozen worden. Hoe hoger de orde van de spline, hoe nauwkeuriger de oplossing. Wegens de ingebouwde continuïteiten is de dimensie van de spline ruimte (dit zijn het aantal vrijheidsgraden) toch beperkt, wat leidt tot kleine discretisatie stelsels.
• Homogene randvoorwaarden gedefinieerd op een willekeurige rand kunnen exact voldaan worden.

Wat komt er zoal aan bod in dit eindwerk:

• Implementatie van de WEB-spline eindige elementenmethode.
• Vergelijking van WEB-splines met andere conventionele eindige elementen, o.a. Lagrange, Clough-Tocher, Powell-Sabin elementen.
• Hoe kiezen we een geschikte gewichtsfunctie? Kunnen we op een gelijkaardige manier niet-homogene randvoorwaarden aangepakken?
• Eventuele uitbreiding naar 3D differentiaalvergelijkingen.