Masterproef T801 : Canonieke Polyadische Decompositie van Hogere-Orde Tensoren: Algoritme en Toepassing

Informatie:	Lieven De Lathauwe	Marc Van Barel
Promotor:	Lieven De Lathauwe (kulak)	Marc Van Barel
Begeleider:	Laurent Sorber

Numerieke Approximatie en Lineaire Algebra Groep

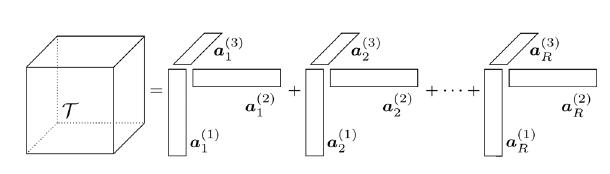
Een basisvraagstuk uit de lineaire algebra is hoeveel rang‐1 termen er nodig zijn om een gegeven matrix voor te stellen en hoe deze kunnen bepaald worden. Het aantal is de rang van de matrix, en voor de berekening bestaan er talloze algoritmen. Deze masterproef betreft de ontbinding van een hogere‐orde tensor in een minimaal aantal rang‐1 termen. Hogere‐orde tensoren zijn het hogere‐orde equivalent van vectoren (eerste orde) en matrices (tweede orde). Ze kunnen intuïtief worden beschouwd als “blokken” van getallen, in drie of meer dimensies. Tensortechnieken zijn de laatste decennia sterk in opmars in signaalverwerking, gegevensontginning, systeemtheorie, wetenschappelijk rekenen, ... Het aantal vereiste termen is de rang van de tensor en de ontbinding wordt Canonieke Polyadische Decompositie (CPD) genoemd. Het CPD probleem is een basisprobleem, relevant over het hele spectrum van zeer fundamenteel tot zeer toegepast. Onder bepaalde voorwaarden op rang en dimensies is de oplossing gekend. Voor een groot stuk is het terrein echter nog onontgonnen. De bekomen resultaten hebben reeds talrijke toepassingen evonden in signaalverwerking, biomedische ingenieurstechnieken, telecommunicatie, het ontginnen van etwerk en hyperlink gegevens, chemometrie, wetenschappelijk rekenen, enz.

De bedoeling van de masterproef is het ontwikkelen van een algoritme voor de berekening van de CPD dat qua werkhypotheses minder beperkend is dan de bestaande algoritmen, en de toepassing ervan op ingenieursproblemen.

Het werk omvat een literatuurstudie, de ontwikkeling van een nieuw algebraïsch resultaat en bijhorend numeriek algoritme, de implementatie ervan in Matlab, en het testen en toepassen op realistische signalen.

Afhankelijk van de interesse van de student kan er meer de nadruk gelegd worden op algebraïsche aspecten, op ontwikkeling en implementatie van algoritmen of op het uitwerken van toepassingen.

Deze masterproef is voor 1 student.