Masterproef T804 : NLEP-Contour: Het oplossen van niet-lineaire eigenwaardeproblemen via contour-integratie

Begeleiding:

Informatie:	Marc Van Barel
Promotoren:	Marc Van Barel	Wim Michiels
Begeleider:	Marc Van Barel

Onderzoeksgroep:

Numerieke Approximatie en Lineaire Algebra Groep en Technisch Wetenschappelijk Rekenen

Context:

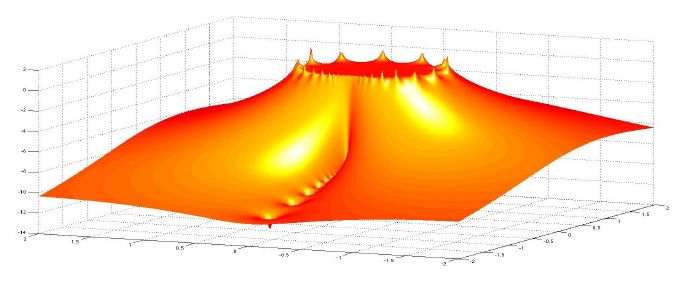
Niet-lineaire eigenwaardeproblemen vormen op dit ogenblik een belangrijk onderzoeksdomein binnen de wiskundige ingenieurstechnieken. Verschillende modellen geven aanleiding tot het volgende probleem: gegeven een analytische m xm matrix-functie T(z) , zoek alle eigenwaarden λ en eventueel bijhorende eigenvectoren v in een bepaald domein van het complexe vlak zodat T(λ)v=0.

Omdat m groot kan zijn, is het belangrijk om het oorspronkelijke grote probleem te reduceren tot een veel kleiner probleem waarbij de grootte afhangt van het aantal eigenwaarden dat gelegen is in het domein van het complexe vlak dat ons interesseert.

Deze compressie kan gebeuren met behulp van contour integratie in het complexe vlak. Het gereduceerde probleem kan dan opgelost worden via bestaande technieken.

Doel:

De bedoeling van de masterproef is het ontwikkelen van de theorie en de algoritmen om op een efficiënte en nauwkeurige manier grote niet-lineaire eigenwaardeproblemen te reduceren tot kleinere problemen en deze gecomprimeerde problemen dan op te lossen via verschillende technieken.

Uitwerking:

Het werk omvat een literatuurstudie, de ontwikkeling van de theorie en bijhorende numerieke methodes, de implementatie ervan in Matlab, en het testen en toepassen op een aantal realistische voorbeelden.

Profiel:

Afhankelijk van de interesse van de student kan er meer de nadruk gelegd worden op theoretische aspecten, op ontwikkeling en implementatie van algoritmen of op het uitwerken van toepassingen.

Deze masterproef is voor 1 student.